At Digital Twin Lab, we conduct foundational mathematical research on digital twins in applied sciences, developing computational methods for complex, nonlinear dynamical systems governed by multiscale and multiphysics processes. We are particularly interested in fast, scalable, and generalizable methods for scientific machine learning and data assimilation, especially for inverse problems in canonical turbulent flows across a wide range of spatial and temporal scales. Our efforts center on hybrid analysis and modeling within large eddy simulation and reduced order modeling frameworks, integrating physics-based and data-driven modeling for emerging digital twin technologies. We further extend these capabilities through scientific AI applications in aerospace and Earth sciences, where machine learning and advanced inference methods enhance turbulence modeling, improve predictive capability, facilitate uncertainty quantification, and enable scalable digital twin frameworks for complex physical systems.
Digital Twin (DT)
The rapid pace of digitalization has led to the rise of digital twin technologies, evolving computational models that mirror physical assets or processes. Digital twins both predict and control real systems while continuously calibrating models with real-time data. With applications spanning the entire asset lifecycle, the digital twin concept is projected to sustain a multibillion-dollar market for years to come.
Hybrid Analysis and Modeling (HAM)
In the modeling landscape, two primary approaches are considered: physics-based and data-driven. Physics-based models are grounded in first principles, providing high generalizability and trustworthiness. Data-driven models, by contrast, seek to explain phenomena through statistical learning from archival data. While deep learning has achieved human-level performance in many tasks and offers advantages such as online learning and computational efficiency, it can suffer from data hunger, limited generalizability, and a lack of robust stability theory, especially in multiscale and multiphysics systems. To overcome these limitations, we develop HAM approaches that synergistically combine deterministic and statistical components.
Dynamic Data Assimilation (DDA)
Data assimilation integrates models and observations to improve predictive accuracy across complex systems. However, the high computational cost of repeatedly solving physics-based models poses a major challenge. To address this, we explore machine-learning-based surrogate models that learn directly from data, providing fast and efficient alternatives that can accelerate and enhance the data assimilation process.
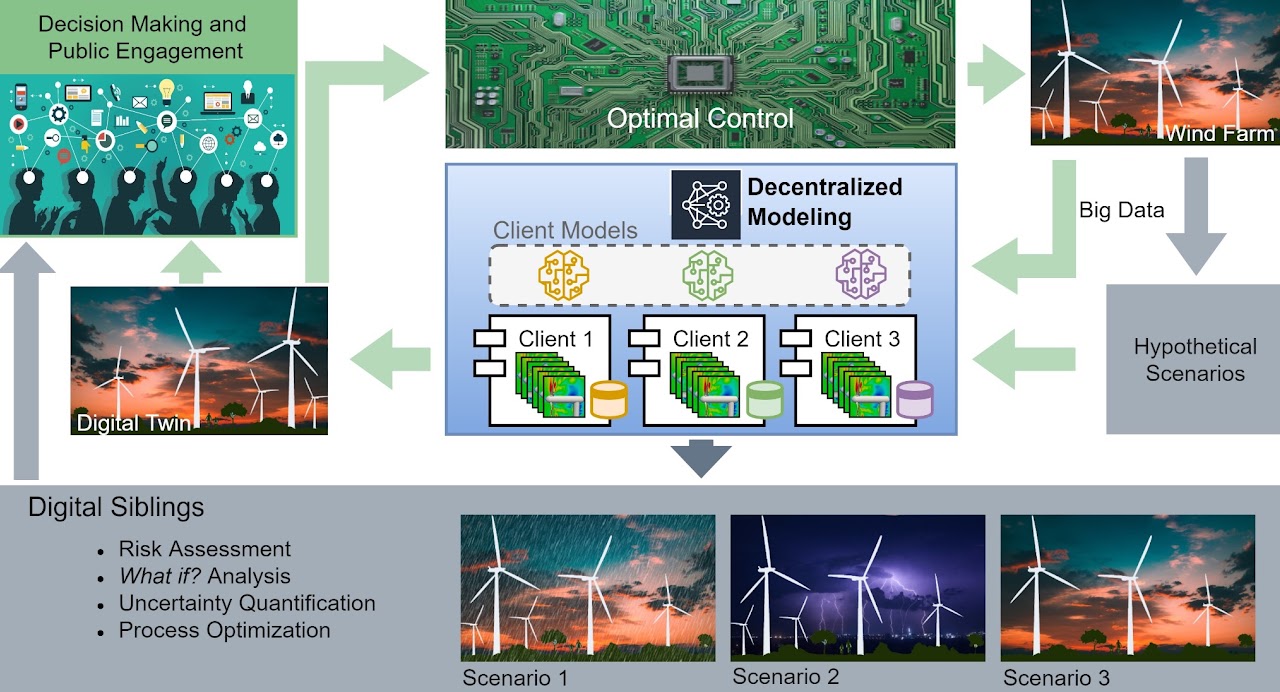
Large Language Models for Control (LLMC)
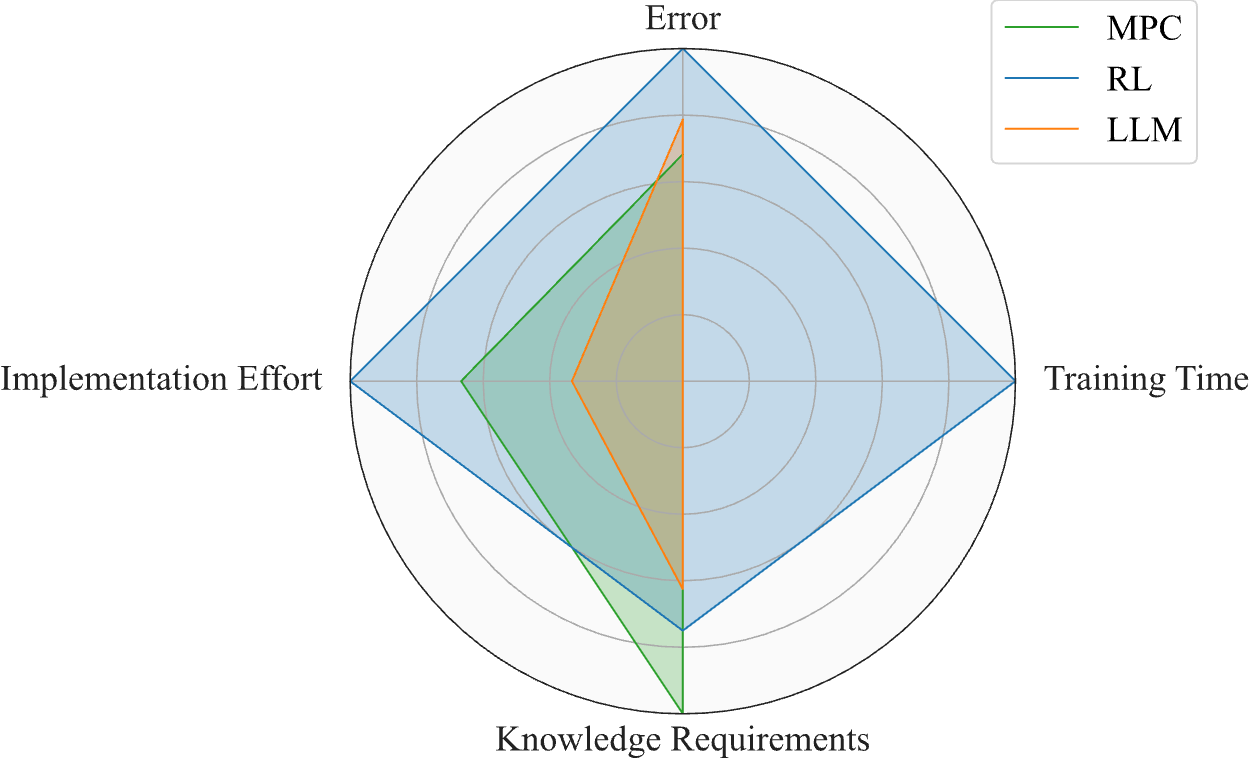
Advances in reinforcement learning (RL), causal modeling, and multimodal perception are bringing to life the long-envisioned idea of cognitive twins, intelligent systems that think, perceive, and act alongside humans. Large Language Models (LLMs) play a central role by interpreting unstructured data, defining goals, and communicating naturally with operators. When integrated with physics-based models and domain simulators, LLM-driven agents can reason about scenarios, explain outcomes, and adapt strategies through human feedback. Inspired by model predictive control (MPC) in the age of generative AI, these capabilities enable intelligent, interpretable, and trustworthy autonomous systems.
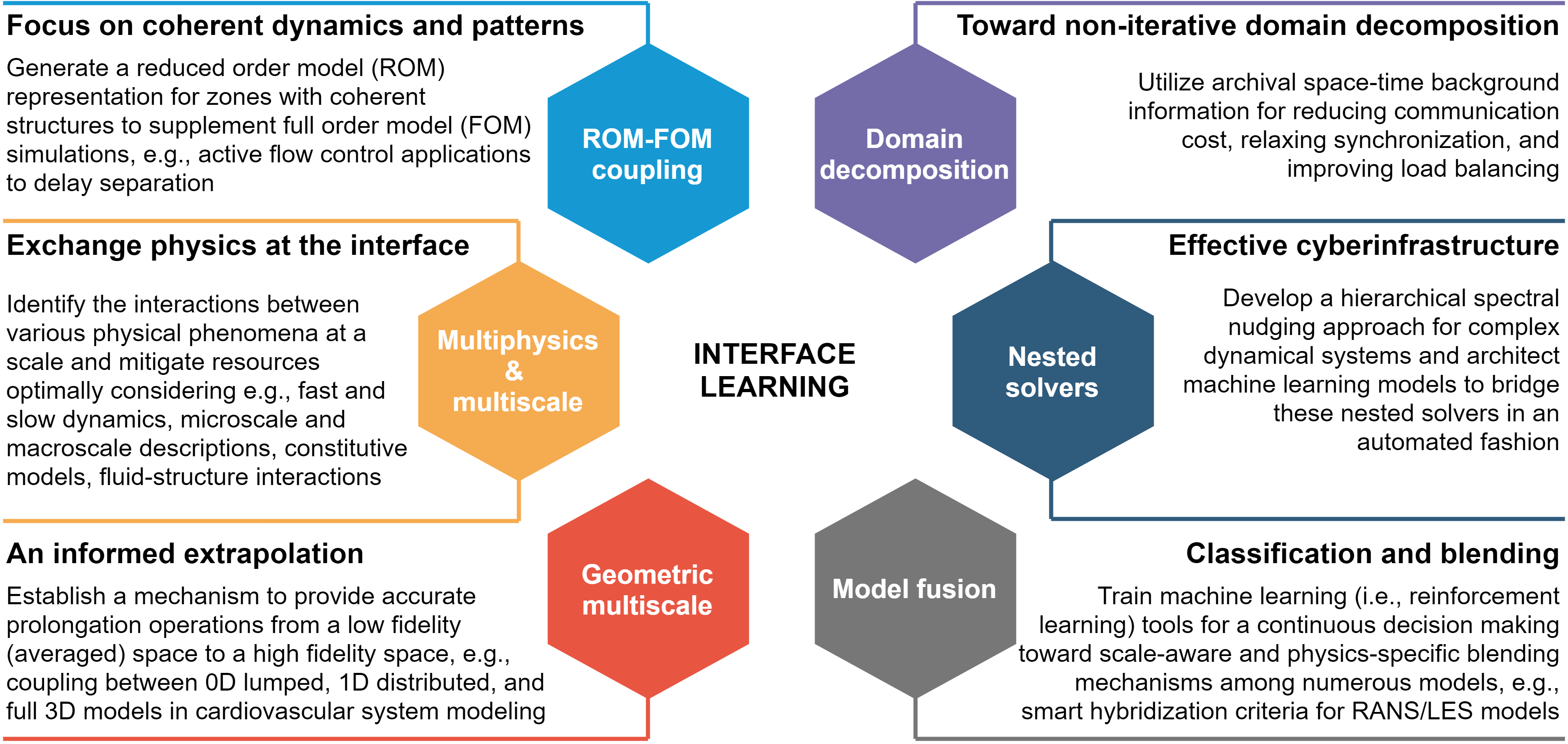
Interface Learning (IL)
Despite advances in scientific computing, high-fidelity simulations remain limited by dimensional complexity. Our lab develops machine learning methods to learn interface boundary conditions without resolving full domains, minimizing inter-region communication and enabling efficient modeling of information exchange at interfaces across science and engineering.

Machine Learning for Fluid Dynamics (MLFD)
Advances in computation and data have transformed modeling approaches across science and engineering. Our lab develops physics-guided machine learning frameworks to identify nonlinear relationships in turbulent flows and build reliable closure models for large eddy simulations (LES). By integrating data-driven and physics-based strategies, we create subgrid-scale models consistent with direct numerical simulations (DNS). Our recent effort focuses on developing accurate and structure-invariant super-resolution approaches to link coarse-grained data with LES and DNS, aiming to advance predictive technologies for turbulence, weather, and climate modeling.
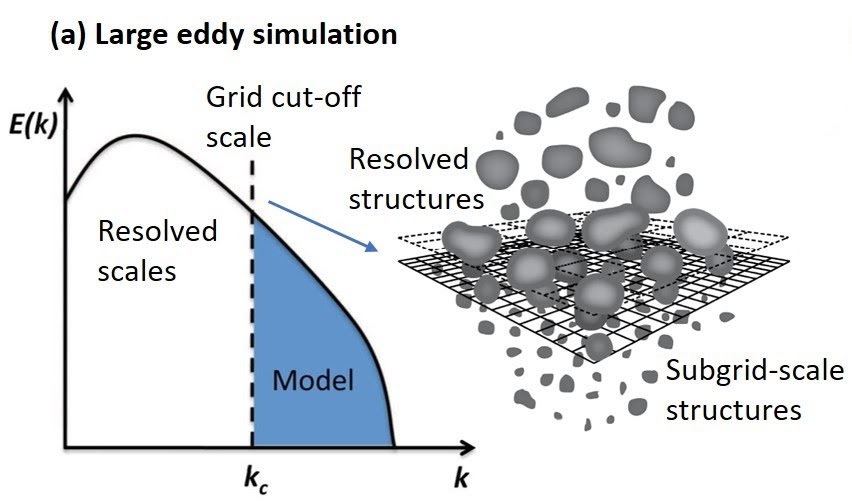
Large Eddy Simulations (LES)
Large eddy simulation (LES), a successful approach for turbulent flow simulation, decomposes the flow into large and small scales through spatial low-pass filtering. The nonlinearity of the governing equations leads to a well-known closure problem. Our work develops functional, structural, and data-driven closure modeling techniques to address subgrid-scale effects in LES, incorporating truncated scales into resolved dynamics to account for missing physics. This is crucial for nonlinear dynamical processes with strong multiscale interactions.
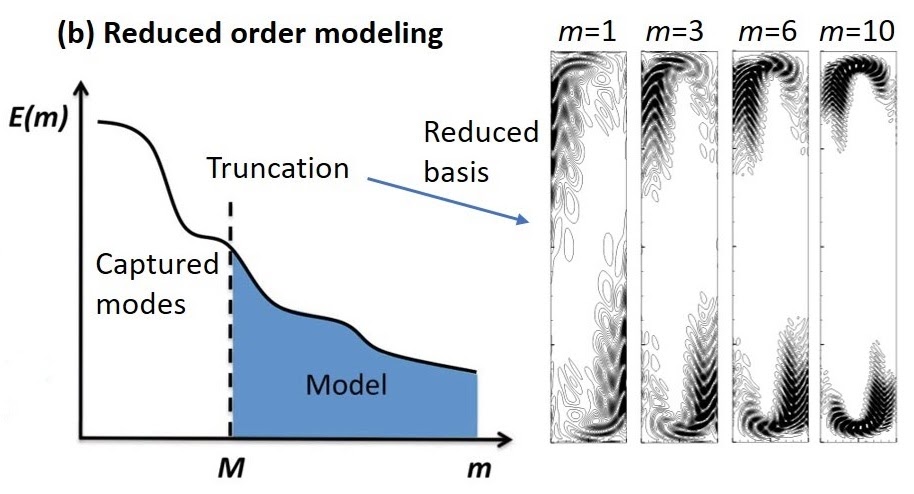
Reduced Order Modeling (ROM)
Reduced order models are highly efficient, low-dimensional representations that can reduce the computational cost of high-fidelity models by orders of magnitude, especially when many evaluations are required across wide parameter ranges. Achieving accuracy requires addressing the closure problem, broadly encompassing missing physics, model uncertainty, and representation limitations. We model the impact of discarded modes on the resolved dynamics to develop precise, reliable low-dimensional models for complex problems.